Estimation of Simple SBMs

Source: R/estimate.R

This function performs variational inference of simple Stochastic Block Models, with various model for the distribution of the edges: Bernoulli, Poisson, or Gaussian models.

estimateSimpleSBM(
  netMat,
  model = "bernoulli",
  directed = !isSymmetric(netMat),
  dimLabels = c("node"),
  covariates = list(),
  estimOptions = list()
)

Arguments

netMat

a matrix describing the network: either an adjacency (square) or incidence matrix with possibly weighted entries.

model

character describing the model for the relation between nodes ('bernoulli', 'poisson', 'gaussian', ...). Default is 'bernoulli'.

directed

logical: is the network directed or not? Only relevant when type is 'Simple'. Default is TRUE if netMat is symmetric, FALSE otherwise

dimLabels

an optional label for referring to the nodes

covariates

a list of matrices with same dimension as mat describing covariates at the edge level. No covariate per Default.

estimOptions

a list of parameters controlling the inference algorithm and model selection. See details.

Value

a list with the estimated parameters. See details...

Details

The list of parameters estimOptions essentially tunes the optimization process and the variational EM algorithm, with the following parameters

  • "nbCores integer for number of cores used. Default is 2

  • "verbosity" integer for verbosity (0, 1). Default is 1

  • "plot" boolean, should the ICL by dynamically plotted or not. Default is TRUE

  • "exploreFactor" control the exploration of the number of groups

  • "exploreMin" explore at least until exploreMin even if the exploration factor rule is achieved. Default 4. See the package blockmodels for details.

  • "exploreMax" Stop exploration at exploreMax even if the exploration factor rule is not achieved. Default Inf. See the package blockmodels for details.

  • "nbBlocksRange" minimal and maximal number or blocks explored

  • "fast" logical: should approximation be used for Bernoulli model with covariates. Default to TRUE

Examples

### =======================================
### SIMPLE BINARY SBM (Bernoulli model)

## Graph parameters & Sampling
nbNodes  <- 60
blockProp <- c(.5, .25, .25) # group proportions
means <- diag(.4, 3) + 0.05  # connectivity matrix: affiliation network
connectParam <- list(mean = means)
mySampler <- sampleSimpleSBM(nbNodes, blockProp, connectParam)
adjacencyMatrix <- mySampler$networkData

## Estimation
mySimpleSBM <-
  estimateSimpleSBM(adjacencyMatrix, 'bernoulli', estimOptions = list(plot = FALSE))
#> -> Estimation for 1 groups
#> 
-> Computation of eigen decomposition used for initalizations
#> 
#> -> Pass 1
#>     -> With ascending number of groups
#>         -> For 2 groups
#> 
        -> For 3 groups
#> 
        -> For 4 groups
#> 
        -> For 5 groups
#> 
    -> With descending number of groups
#>         -> For 4 groups
#> 

        -> For 3 groups
#> 
        -> For 2 groups
#> 
-> Pass 2
#>     -> With ascending number of groups
#>         -> For 2 groups
#>         -> For 3 groups
#>         -> For 4 groups
#>         -> For 5 groups
#>     -> With descending number of groups
#>         -> For 4 groups
#>         -> For 3 groups
#>         -> For 2 groups
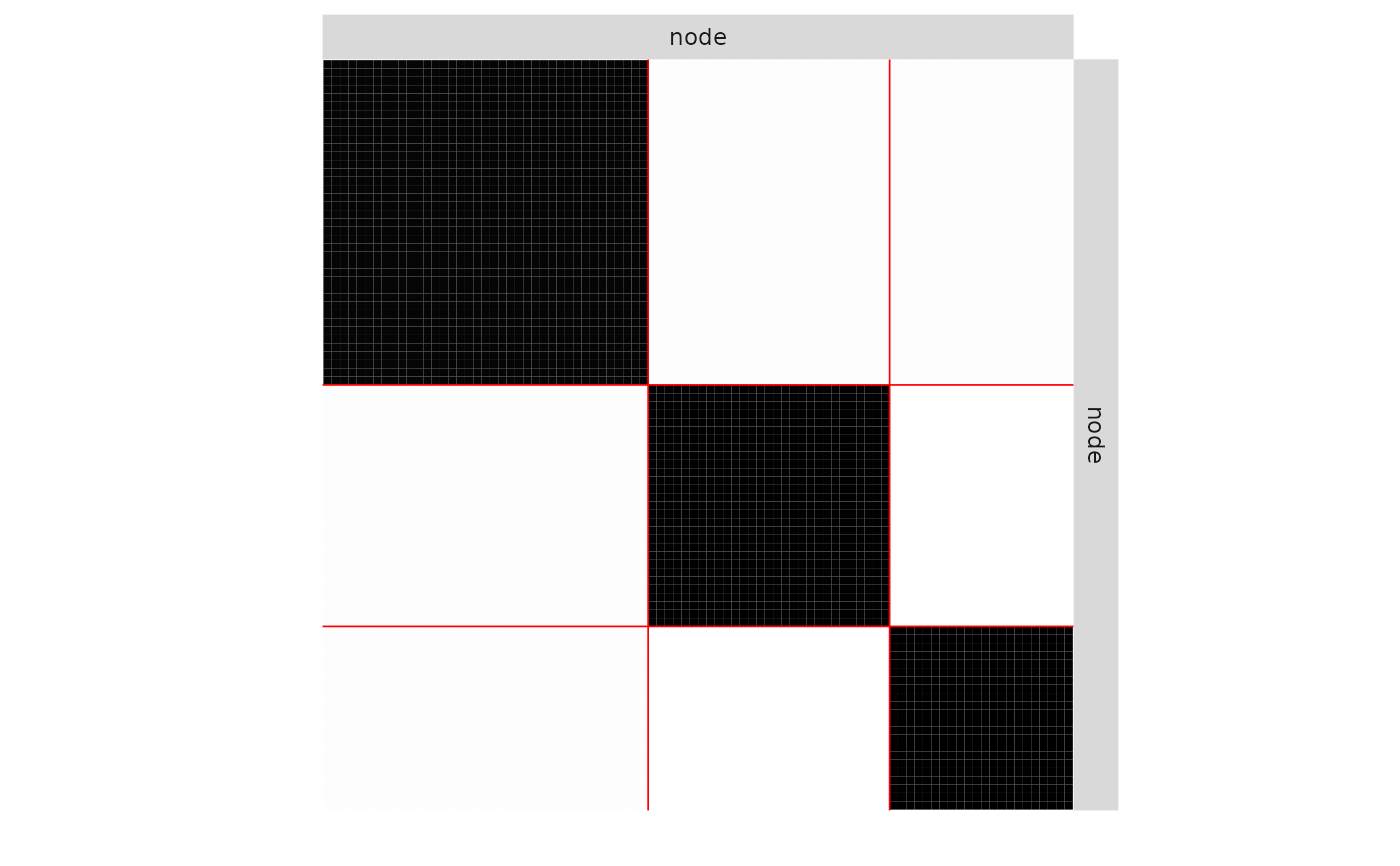
plot(mySimpleSBM, 'data', ordered = FALSE)

plot(mySimpleSBM, 'data')

plot(mySimpleSBM, 'expected', ordered = FALSE)

plot(mySimpleSBM, 'expected')

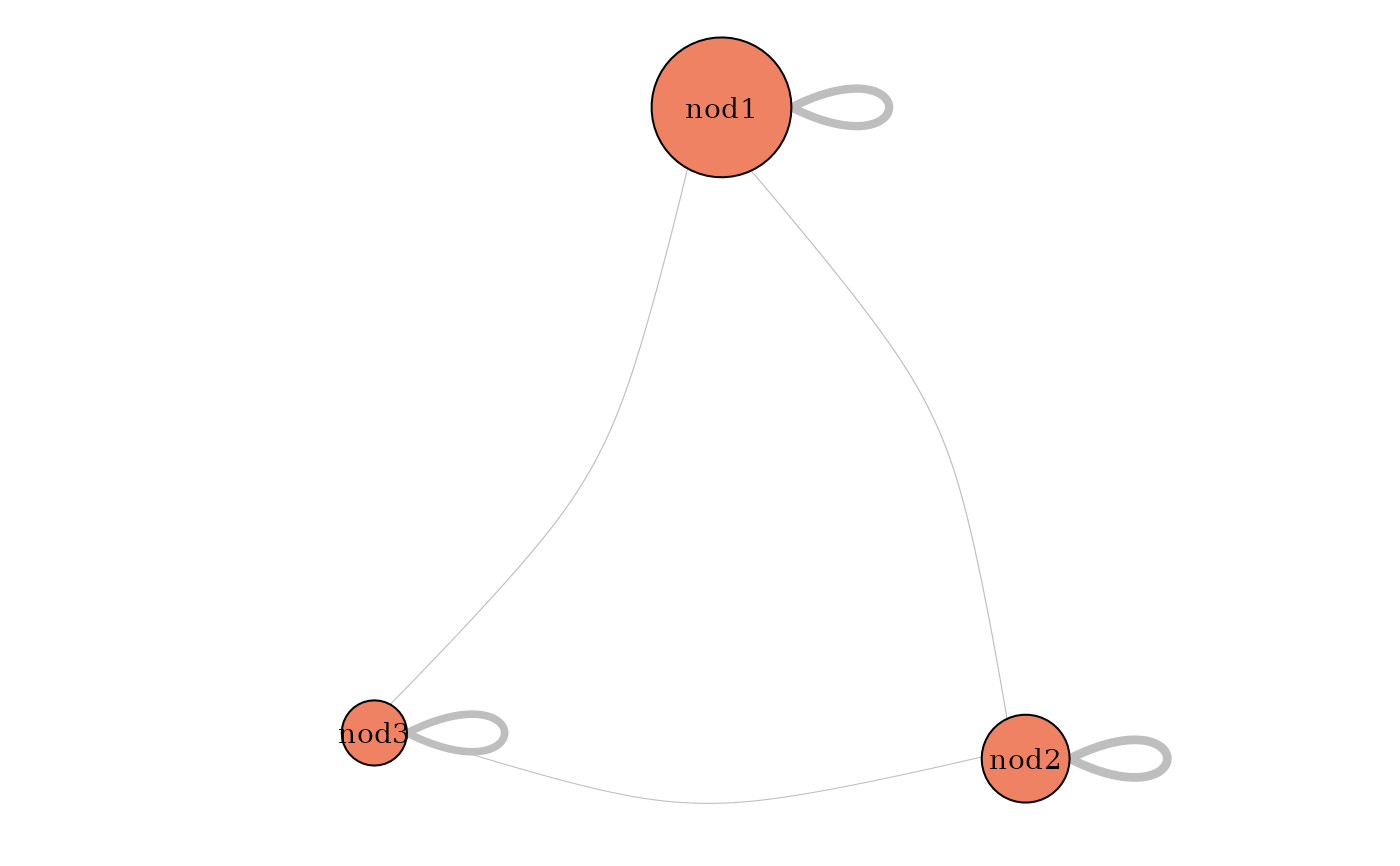
plot(mySimpleSBM, 'meso')


### =======================================
### SIMPLE POISSON SBM

## Graph parameters & Sampling
nbNodes  <- 60
blockProp <- c(.5, .25, .25) # group proportions
means <- diag(15., 3) + 5    # connectivity matrix: affiliation network
connectParam <- list(mean = means)
mySampler <- sampleSimpleSBM(nbNodes, blockProp, list(mean = means), model = "poisson")
adjacencyMatrix <- mySampler$networkData

## Estimation
mySimpleSBM <- estimateSimpleSBM(adjacencyMatrix, 'poisson',
   estimOptions = list(plot = FALSE))
#> -> Estimation for 1 groups
#> 
-> Computation of eigen decomposition used for initalizations
#> 
#> -> Pass 1
#>     -> With ascending number of groups
#>         -> For 2 groups
#> 
        -> For 3 groups
#> 
        -> For 4 groups
#> 
        -> For 5 groups
#> 
    -> With descending number of groups
#>         -> For 4 groups
#> 

        -> For 3 groups
#> 
        -> For 2 groups
#> 
-> Pass 2
#>     -> With ascending number of groups
#>         -> For 2 groups
#>         -> For 3 groups
#>         -> For 4 groups
#>         -> For 5 groups
#>     -> With descending number of groups
#>         -> For 4 groups
#>         -> For 3 groups
#>         -> For 2 groups
plot(mySimpleSBM, 'data', ordered = FALSE)

plot(mySimpleSBM, 'data')

plot(mySimpleSBM, 'expected', ordered = FALSE)

plot(mySimpleSBM, 'expected')


### =======================================
### SIMPLE GAUSSIAN SBM

## Graph parameters & Sampling
nbNodes  <- 60
blockProp <- c(.5, .25, .25)      # group proportions
means <- diag(15., 3) + 5 # connectivity matrix: affiliation network
connectParam <- list(mean = means, var = 2)
mySampler <- sampleSimpleSBM(nbNodes, blockProp, connectParam, model = "gaussian")

## Estimation
mySimpleSBM <-
   estimateSimpleSBM(mySampler$networkData, 'gaussian', estimOptions = list(plot = FALSE))
#> -> Estimation for 1 groups
#> 
-> Computation of eigen decomposition used for initalizations
#> 
#> -> Pass 1
#>     -> With ascending number of groups
#>         -> For 2 groups
#> 
        -> For 3 groups
#> 
        -> For 4 groups
#> 
        -> For 5 groups
#> 
    -> With descending number of groups
#>         -> For 4 groups
#> 

        -> For 3 groups
#> 
        -> For 2 groups
#> 
-> Pass 2
#>     -> With ascending number of groups
#>         -> For 2 groups
#>         -> For 3 groups
#>         -> For 4 groups
#>         -> For 5 groups
#>     -> With descending number of groups
#>         -> For 4 groups
#>         -> For 3 groups
#>         -> For 2 groups
plot(mySimpleSBM, 'data', ordered = FALSE)

plot(mySimpleSBM, 'data')

plot(mySimpleSBM, 'expected', ordered = FALSE)

plot(mySimpleSBM, 'expected')