This function performs variational inference of bipartite Stochastic Block Models, with various model for the distribution of the edges: Bernoulli, Poisson, or Gaussian models.
Arguments
- netMat
a matrix describing the network: either an adjacency (square) or incidence matrix with possibly weighted entries.
- model
character describing the model for the relation between nodes (
'bernoulli','poisson','gaussian', ...). Default is'bernoulli'.- dimLabels
an optional vector of labels for each dimension (in row, in column)
- covariates
a list of matrices with same dimension as mat describing covariates at the edge level. No covariate per Default.
- estimOptions
a list of parameters controlling the inference algorithm and model selection. See details.
Value
a list with the estimated parameters. See details...
Details
The list of parameters estimOptions essentially tunes the optimization process and the variational EM algorithm, with the following parameters
"nbCores integer for number of cores used. Default is 2
"verbosity" integer for verbosity (0, 1). Default is 1
"plot" boolean, should the ICL by dynamically plotted or not. Default is TRUE
"exploreFactor" control the exploration of the number of groups
"exploreMin" explore at least until exploreMin even if the exploration factor rule is achieved. Default 4. See the package blockmodels for details.
"exploreMax" Stop exploration at exploreMax even if the exploration factor rule is not achieved. Default Inf. See the package blockmodels for details.
"nbBlocksRange" minimal and maximal number or blocks explored
"fast" logical: should approximation be used for Bernoulli model with covariates. Default to
TRUE
Examples
### =======================================
### BIPARTITE BINARY SBM (Bernoulli model)
## Graph parameters and Sampling
nbNodes <- c(60, 80)
blockProp <- list(c(.5, .5), c(1/3, 1/3, 1/3)) # group proportions
means <- matrix(runif(6), 2, 3) # connectivity matrix
# In Bernoulli SBM, parameters is a list with a
# matrix of means 'mean' which are probabilities of connection
connectParam <- list(mean = means)
mySampler <- sampleBipartiteSBM(nbNodes, blockProp, connectParam, model = 'bernoulli')
## Estimation
myBipartiteSBM <- estimateBipartiteSBM(mySampler$networkData, estimOptions = list(plot = FALSE))
#> -> Estimation for 2 groups (1+1)
#>
-> Computation of eigen decomposition used for initalizations
#> -> for rows
#> -> for cols
#>
#> -> Pass 1
#> -> With ascending number of groups
#> -> For 3 groups
#>
-> For 4 groups
#>
-> For 5 groups
#>
-> For 6 groups
#>
-> For 7 groups
#>
-> For 8 groups
#>
-> With descending number of groups
#> -> For 7 groups
#>
-> For 6 groups
#>
-> For 5 groups
#>
-> For 4 groups
#>
-> For 3 groups
#>
-> Pass 2
#> -> With ascending number of groups
#> -> For 3 groups
#> -> For 4 groups
#> -> For 5 groups
#> -> For 6 groups
#> -> For 7 groups
#>
-> For 8 groups
#>
-> With descending number of groups
#> -> For 7 groups
#>
-> For 6 groups
#>
-> For 5 groups
#>
-> For 4 groups
#> -> For 3 groups
#> -> Pass 3
#> -> With ascending number of groups
#> -> For 3 groups
#> -> For 4 groups
#> -> For 5 groups
#> -> For 6 groups
#> -> For 7 groups
#>
-> For 8 groups
#>
-> With descending number of groups
#> -> For 7 groups
#>
-> For 6 groups
#>
-> For 5 groups
#> -> For 4 groups
#> -> For 3 groups
#> -> Pass 4
#> -> With ascending number of groups
#> -> For 3 groups
#> -> For 4 groups
#> -> For 5 groups
#> -> For 6 groups
#> -> For 7 groups
#> -> For 8 groups
#> -> With descending number of groups
#> -> For 7 groups
#> -> For 6 groups
#> -> For 5 groups
#> -> For 4 groups
#> -> For 3 groups
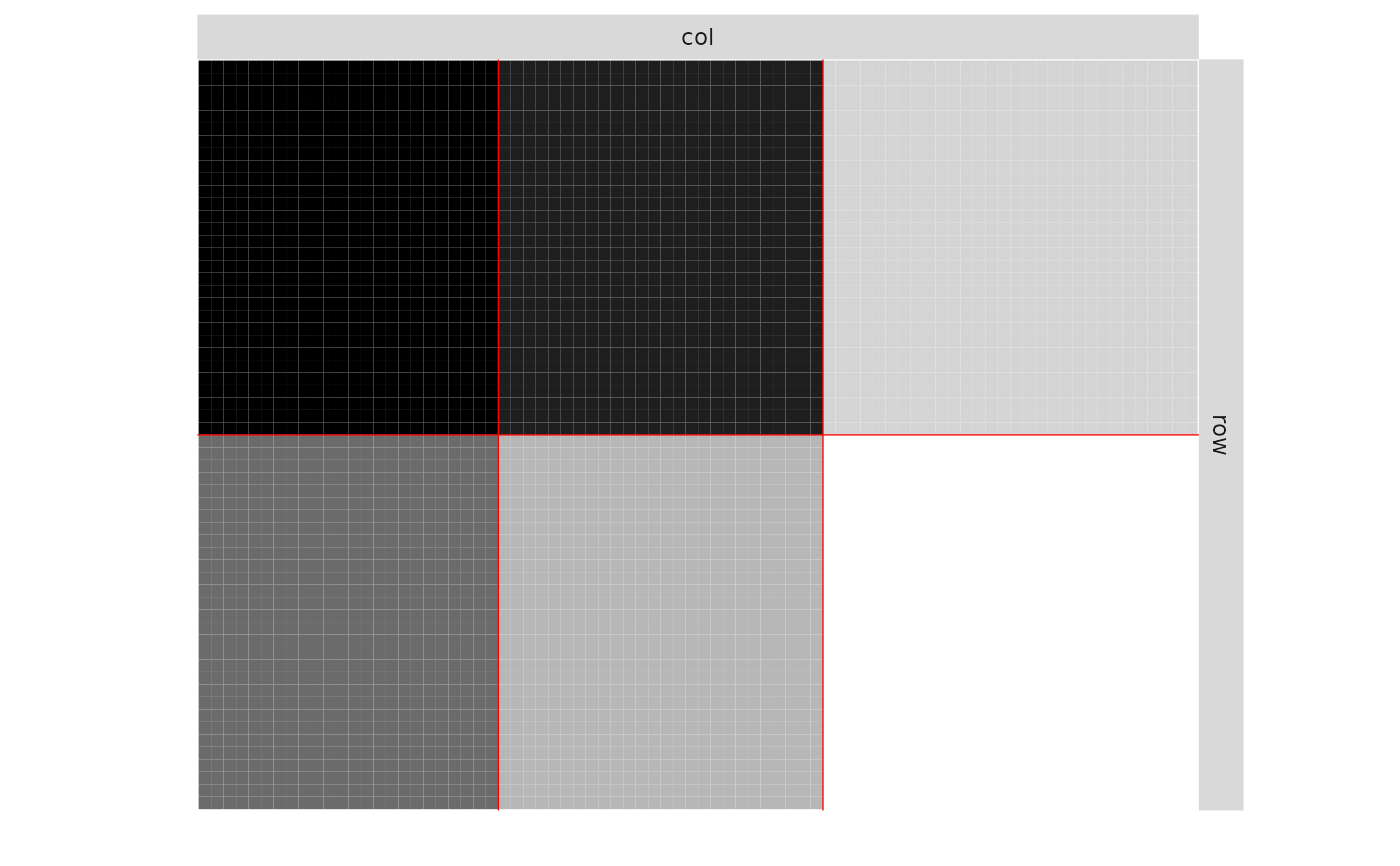
plot(myBipartiteSBM, 'expected')
 ### =======================================
### BIPARTITE POISSON SBM
## Graph parameters & Sampling
nbNodes <- c(60, 80)
blockProp <- list(c(.5, .5), c(1/3, 1/3, 1/3)) # group proportions
means <- matrix(rbinom(6, 30, 0.25), 2, 3) # connectivity matrix
connectParam <- list(mean = means)
mySampler <- sampleBipartiteSBM(nbNodes, blockProp, connectParam, model = 'poisson')
## Estimation
myBipartiteSBM <-
estimateBipartiteSBM(mySampler$networkData, 'poisson', estimOptions = list(plot = FALSE))
#> -> Estimation for 2 groups (1+1)
#>
-> Computation of eigen decomposition used for initalizations
#> -> for rows
#> -> for cols
#>
#> -> Pass 1
#> -> With ascending number of groups
#> -> For 3 groups
#>
-> For 4 groups
#>
-> For 5 groups
#>
-> For 6 groups
#>
-> For 7 groups
#>
-> For 8 groups
#>
-> With descending number of groups
#> -> For 7 groups
#>
-> For 6 groups
#>
-> For 5 groups
#>
-> For 4 groups
#>
-> For 3 groups
#>
-> Pass 2
#> -> With ascending number of groups
#> -> For 3 groups
#> -> For 4 groups
#> -> For 5 groups
#> -> For 6 groups
#> -> For 7 groups
#>
-> For 8 groups
#>
-> With descending number of groups
#> -> For 7 groups
#> -> For 6 groups
#> -> For 5 groups
#> -> For 4 groups
#> -> For 3 groups
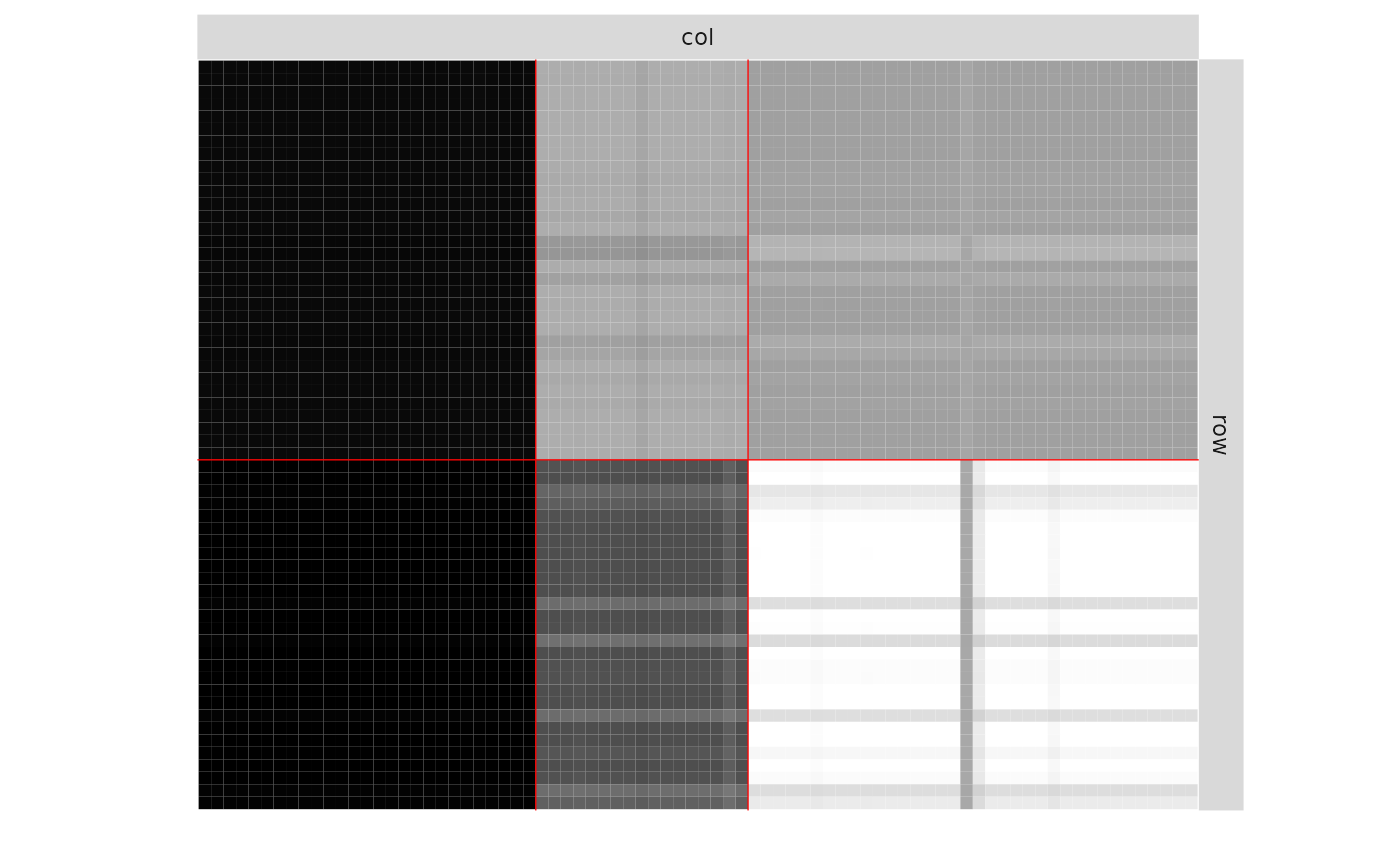
plot(myBipartiteSBM, 'expected')
### =======================================
### BIPARTITE POISSON SBM
## Graph parameters & Sampling
nbNodes <- c(60, 80)
blockProp <- list(c(.5, .5), c(1/3, 1/3, 1/3)) # group proportions
means <- matrix(rbinom(6, 30, 0.25), 2, 3) # connectivity matrix
connectParam <- list(mean = means)
mySampler <- sampleBipartiteSBM(nbNodes, blockProp, connectParam, model = 'poisson')
## Estimation
myBipartiteSBM <-
estimateBipartiteSBM(mySampler$networkData, 'poisson', estimOptions = list(plot = FALSE))
#> -> Estimation for 2 groups (1+1)
#>
-> Computation of eigen decomposition used for initalizations
#> -> for rows
#> -> for cols
#>
#> -> Pass 1
#> -> With ascending number of groups
#> -> For 3 groups
#>
-> For 4 groups
#>
-> For 5 groups
#>
-> For 6 groups
#>
-> For 7 groups
#>
-> For 8 groups
#>
-> With descending number of groups
#> -> For 7 groups
#>
-> For 6 groups
#>
-> For 5 groups
#>
-> For 4 groups
#>
-> For 3 groups
#>
-> Pass 2
#> -> With ascending number of groups
#> -> For 3 groups
#> -> For 4 groups
#> -> For 5 groups
#> -> For 6 groups
#> -> For 7 groups
#>
-> For 8 groups
#>
-> With descending number of groups
#> -> For 7 groups
#> -> For 6 groups
#> -> For 5 groups
#> -> For 4 groups
#> -> For 3 groups
plot(myBipartiteSBM, 'expected')
 ### =======================================
### BIPARTITE GAUSSIAN SBM
## Graph parameters & sampling
nbNodes <- c(60, 80)
blockProp <- list(c(.5, .5), c(1/3, 1/3, 1/3)) # group proportions
means <- 20 * matrix(runif(6), 2, 3) # connectivity matrix
connectParam <- list(mean = means, var = 1)
mySampler <- sampleBipartiteSBM(nbNodes, blockProp, connectParam, model = 'gaussian')
## Estimation
myBipartiteSBM <-
estimateBipartiteSBM(mySampler$networkData, 'gaussian', estimOptions = list(plot = FALSE))
#> -> Estimation for 2 groups (1+1)
#>
-> Computation of eigen decomposition used for initalizations
#> -> for rows
#> -> for cols
#>
#> -> Pass 1
#> -> With ascending number of groups
#> -> For 3 groups
#>
-> For 4 groups
#>
-> For 5 groups
#>
-> For 6 groups
#>
-> For 7 groups
#>
-> For 8 groups
#>
-> With descending number of groups
#> -> For 7 groups
#>
-> For 6 groups
#>
-> For 5 groups
#>
-> For 4 groups
#>
-> For 3 groups
#>
-> Pass 2
#> -> With ascending number of groups
#> -> For 3 groups
#> -> For 4 groups
#> -> For 5 groups
#> -> For 6 groups
#> -> For 7 groups
#>
-> For 8 groups
#>
-> With descending number of groups
#> -> For 7 groups
#> -> For 6 groups
#> -> For 5 groups
#> -> For 4 groups
#> -> For 3 groups
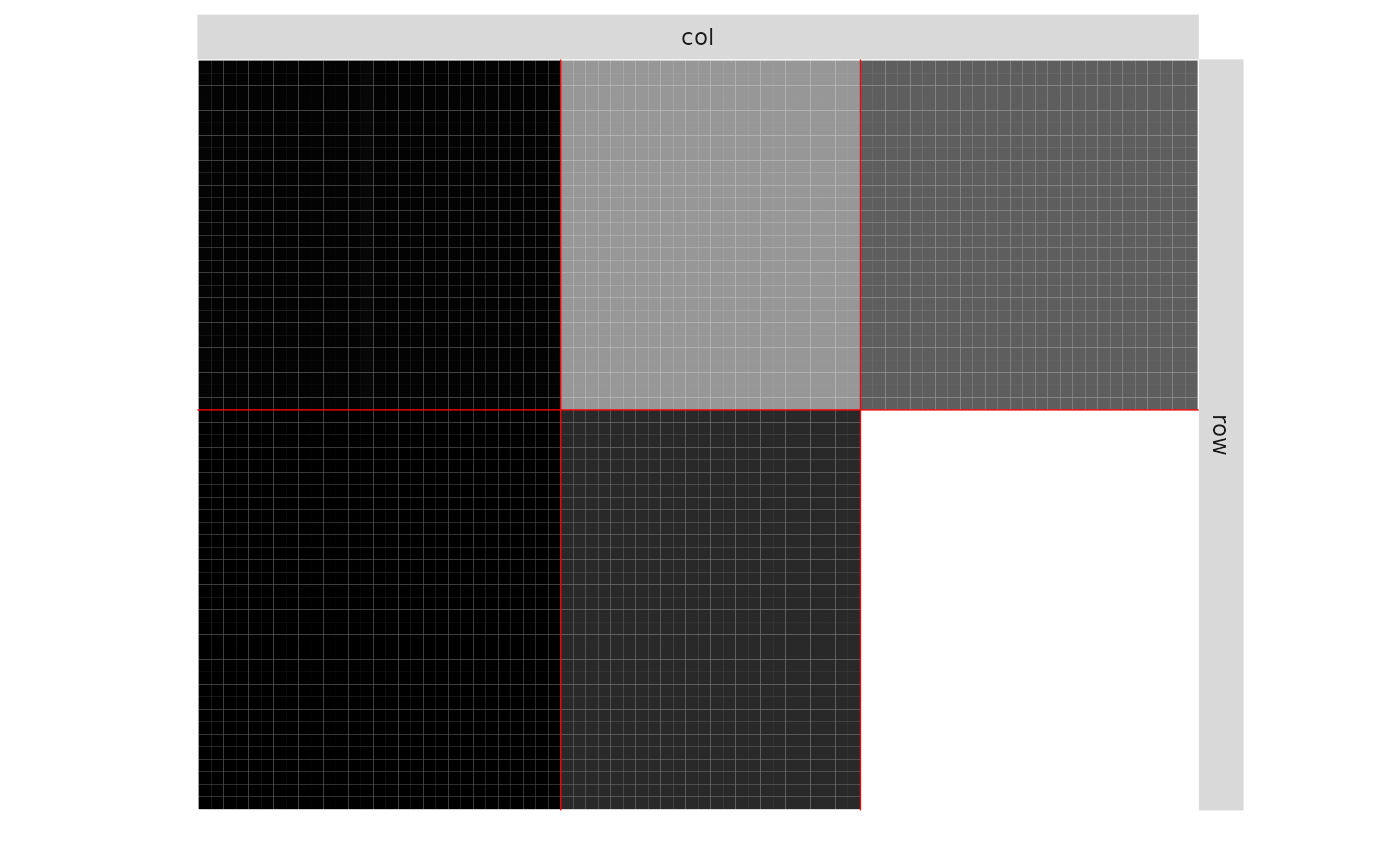
plot(myBipartiteSBM, 'expected')
### =======================================
### BIPARTITE GAUSSIAN SBM
## Graph parameters & sampling
nbNodes <- c(60, 80)
blockProp <- list(c(.5, .5), c(1/3, 1/3, 1/3)) # group proportions
means <- 20 * matrix(runif(6), 2, 3) # connectivity matrix
connectParam <- list(mean = means, var = 1)
mySampler <- sampleBipartiteSBM(nbNodes, blockProp, connectParam, model = 'gaussian')
## Estimation
myBipartiteSBM <-
estimateBipartiteSBM(mySampler$networkData, 'gaussian', estimOptions = list(plot = FALSE))
#> -> Estimation for 2 groups (1+1)
#>
-> Computation of eigen decomposition used for initalizations
#> -> for rows
#> -> for cols
#>
#> -> Pass 1
#> -> With ascending number of groups
#> -> For 3 groups
#>
-> For 4 groups
#>
-> For 5 groups
#>
-> For 6 groups
#>
-> For 7 groups
#>
-> For 8 groups
#>
-> With descending number of groups
#> -> For 7 groups
#>
-> For 6 groups
#>
-> For 5 groups
#>
-> For 4 groups
#>
-> For 3 groups
#>
-> Pass 2
#> -> With ascending number of groups
#> -> For 3 groups
#> -> For 4 groups
#> -> For 5 groups
#> -> For 6 groups
#> -> For 7 groups
#>
-> For 8 groups
#>
-> With descending number of groups
#> -> For 7 groups
#> -> For 6 groups
#> -> For 5 groups
#> -> For 4 groups
#> -> For 3 groups
plot(myBipartiteSBM, 'expected')