Variational EM inference of Stochastic Block Models indexed by block number from a partially observed network.
Arguments
- adjacencyMatrix
The N x N adjacency matrix of the network data. If
adjacencyMatrixis symmetric, we assume an undirected network with no loop; otherwise the network is assumed to be directed.- vBlocks
The vector of number of blocks considered in the collection.
- sampling
The model used to described the process that originates the missing data: MAR designs ("dyad", "node","covar-dyad","covar-node","snowball") and MNAR designs ("double-standard", "block-dyad", "block-node" , "degree") are available. See details.
- covariates
An optional list with M entries (the M covariates). If the covariates are node-centered, each entry of
covariatesmust be a size-N vector; if the covariates are dyad-centered, each entry ofcovariatesmust be N x N matrix.- control
a list of parameters controlling advanced features. See details.
Value
Returns an R6 object with class missSBM_collection.
Details
Internal functions use future_lapply, so set your plan to 'multisession' or
'multicore' to use several cores/workers.
The list of parameters control tunes more advanced features, such as the
initialization, how covariates are handled in the model, and the variational EM algorithm:
useCov logical. If
covariatesis not null, should they be used for the for the SBM inference (or just for the sampling)? Default is TRUE.clusterInit Initial method for clustering: either a character ("spectral") or a list with
length(vBlocks)vectors, each with sizencol(adjacencyMatrix), providing a user-defined clustering. Default is "spectral". similarity An R x R -> R function to compute similarities between node covariates. Default isl1_similarity, that is, -abs(x-y). Only relevant when the covariates are node-centered (i.e.covariatesis a list of size-N vectors).threshold V-EM algorithm stops stop when an optimization step changes the objective function or the parameters by less than threshold. Default is 1e-2.
maxIter V-EM algorithm stops when the number of iteration exceeds maxIter. Default is 50.
fixPointIter number of fix-point iterations in the V-E step. Default is 3.
exploration character indicating the kind of exploration used among "forward", "backward", "both" or "none". Default is "both".
iterates integer for the number of iterations during exploration. Only relevant when
explorationis different from "none". Default is 1.trace logical for verbosity. Default is TRUE.
The different sampling designs are split into two families in which we find dyad-centered and node-centered samplings. See doi:10.1080/01621459.2018.1562934 for a complete description.
Missing at Random (MAR)
dyad parameter = p = Prob(Dyad(i,j) is observed)
node parameter = p = Prob(Node i is observed)
covar-dyad": parameter = beta in R^M, such that Prob(Dyad (i,j) is observed) = logistic(parameter' covarArray (i,j, .))
covar-node": parameter = nu in R^M such that Prob(Node i is observed) = logistic(parameter' covarMatrix (i,)
snowball": parameter = number of waves with Prob(Node i is observed in the 1st wave)
Missing Not At Random (MNAR)
double-standard parameter = (p0,p1) with p0 = Prob(Dyad (i,j) is observed | the dyad is equal to 0), p1 = Prob(Dyad (i,j) is observed | the dyad is equal to 1)
block-node parameter = c(p(1),...,p(Q)) and p(q) = Prob(Node i is observed | node i is in cluster q)
block-dyad parameter = c(p(1,1),...,p(Q,Q)) and p(q,l) = Prob(Edge (i,j) is observed | node i is in cluster q and node j is in cluster l)
See also
Examples
## SBM parameters
N <- 100 # number of nodes
Q <- 3 # number of clusters
pi <- rep(1,Q)/Q # block proportion
theta <- list(mean = diag(.45,Q) + .05 ) # connectivity matrix
## Sampling parameters
samplingParameters <- .75 # the sampling rate
sampling <- "dyad" # the sampling design
## generate a undirected binary SBM with no covariate
sbm <- sbm::sampleSimpleSBM(N, pi, theta)
## Uncomment to set parallel computing with future
## future::plan("multicore", workers = 2)
## Sample some dyads data + Infer SBM with missing data
collection <-
observeNetwork(sbm$networkData, sampling, samplingParameters) %>%
estimateMissSBM(vBlocks = 1:4, sampling = sampling)
#>
#>
#> Adjusting Variational EM for Stochastic Block Model
#>
#> Imputation assumes a 'dyad' network-sampling process
#>
#> Initialization of 4 model(s).
#> Performing VEM inference
#> Model with 4 blocks.
Model with 2 blocks.
Model with 3 blocks.
Model with 1 blocks.
#> Looking for better solutions
#> Pass 1 Going forward +++
Pass 1 Going backward +++
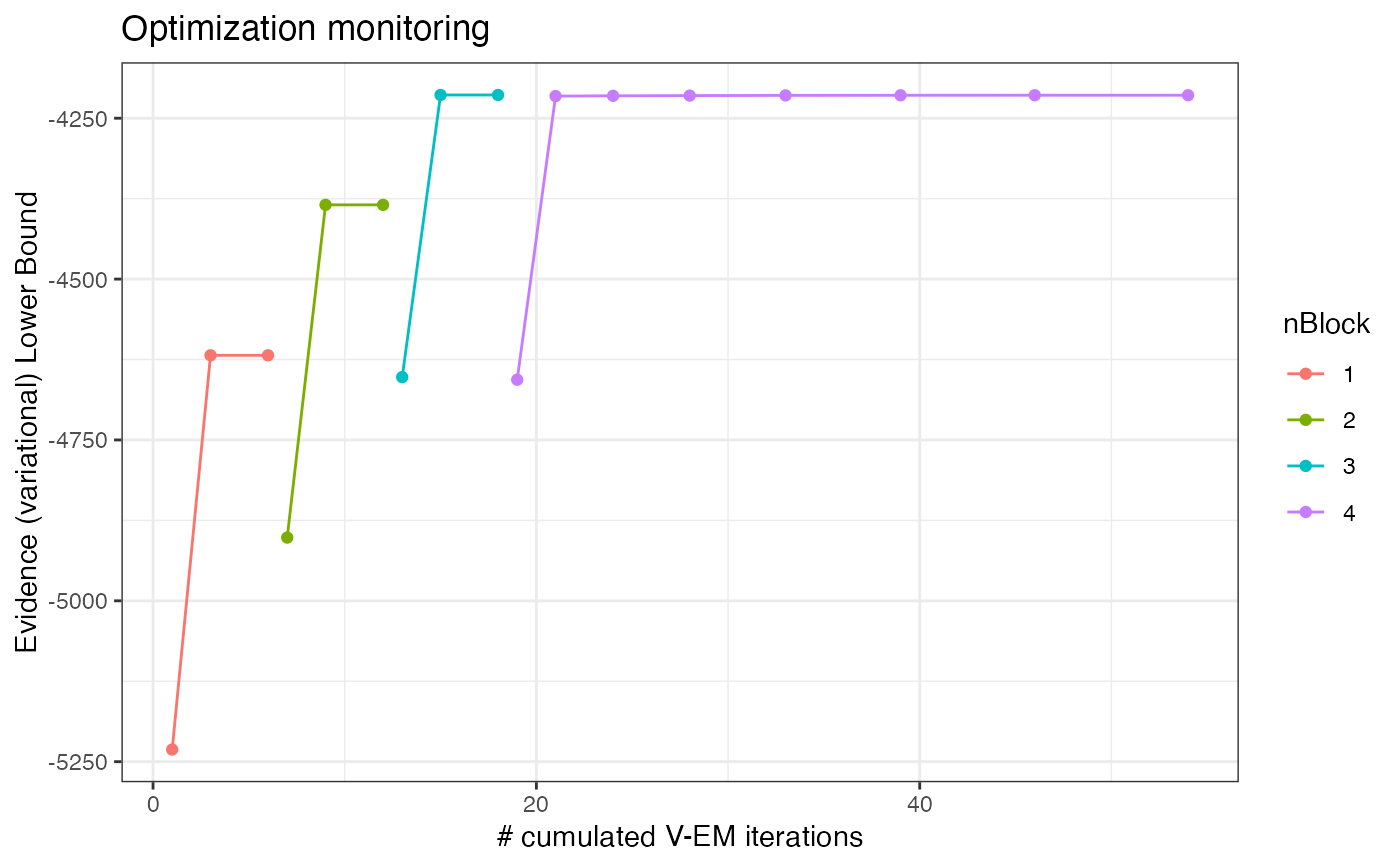
plot(collection, "monitoring")
plot(collection, "icl")
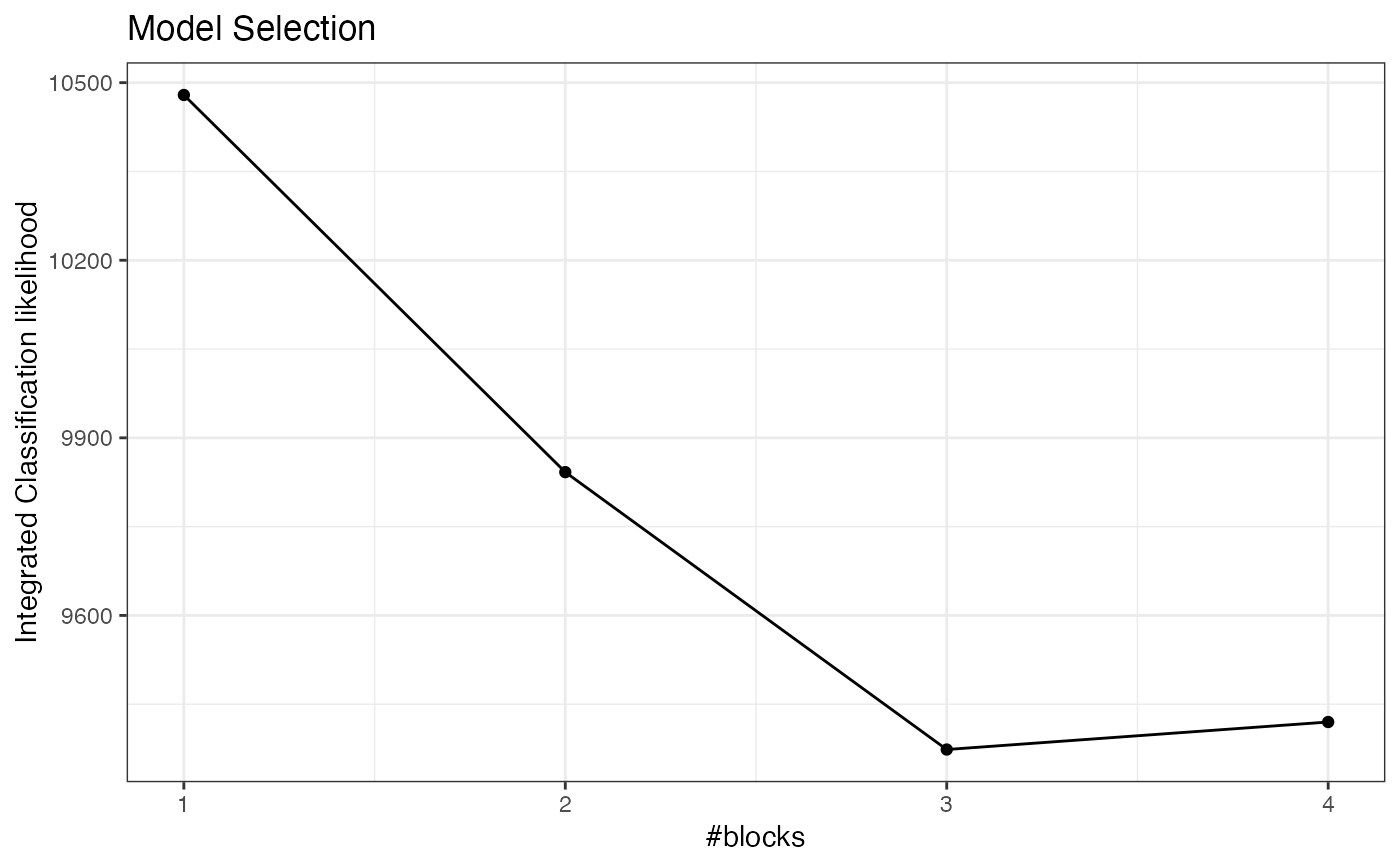collection$ICL
#> [1] 10479.212 9842.056 9373.470 9419.935
coef(collection$bestModel$fittedSBM, "connectivity")
#> $mean
#> [,1] [,2] [,3]
#> [1,] 0.48770657 0.04334042 0.05447533
#> [2,] 0.04334042 0.48648643 0.04308091
#> [3,] 0.05447533 0.04308091 0.52380590
#>
myModel <- collection$bestModel
plot(myModel, "expected")
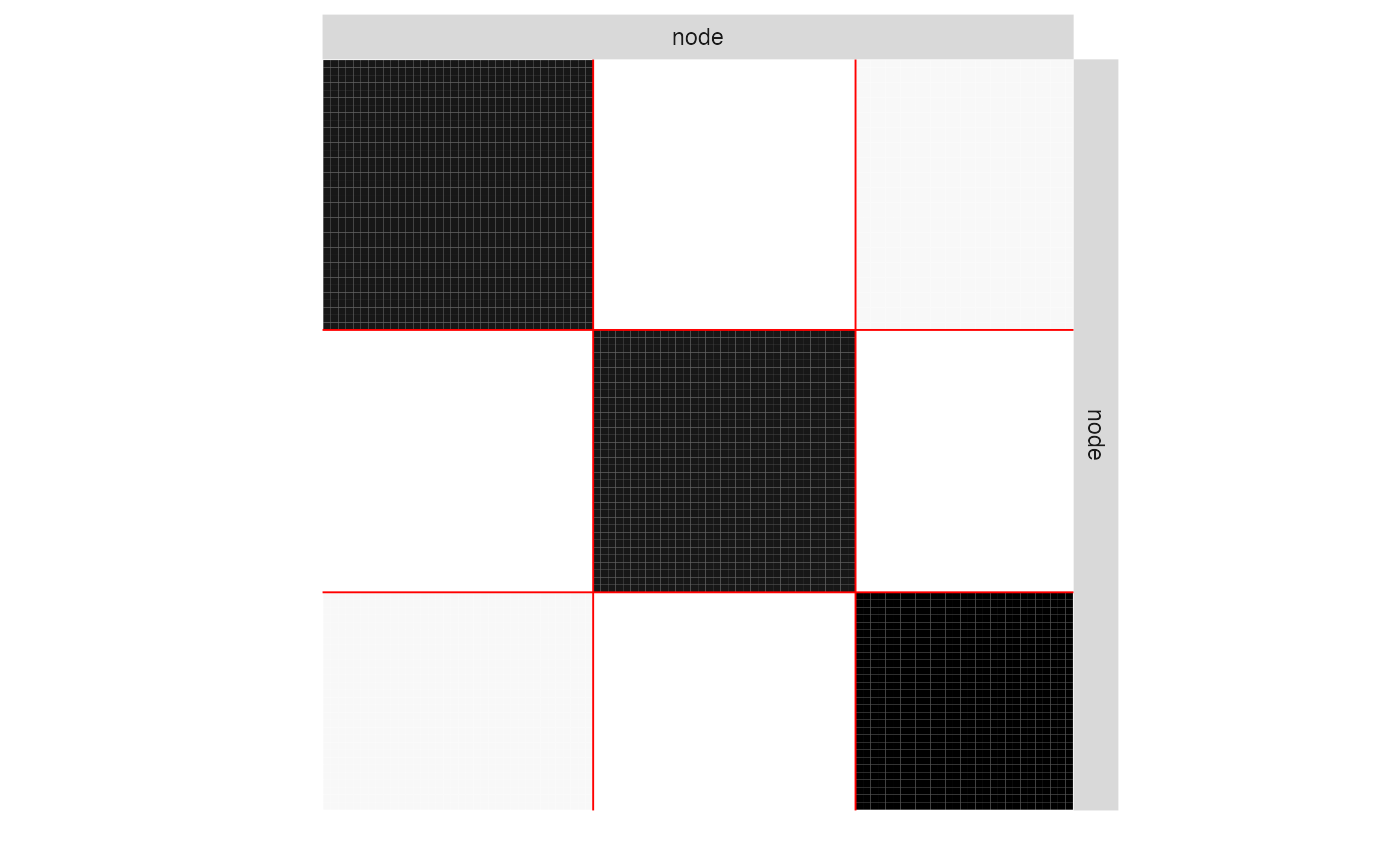plot(myModel, "imputed")
plot(myModel, "meso")
coef(myModel, "sampling")
#> [1] 0.7492929
coef(myModel, "connectivity")
#> $mean
#> [,1] [,2] [,3]
#> [1,] 0.48770657 0.04334042 0.05447533
#> [2,] 0.04334042 0.48648643 0.04308091
#> [3,] 0.05447533 0.04308091 0.52380590
#>
predict(myModel)[1:5, 1:5]
#> 5 x 5 sparse Matrix of class "dgCMatrix"
#>
#> [1,] . . 0.4877066 . .
#> [2,] . . 1.0000000 0.48770657 0.05447533
#> [3,] 0.4877066 1.00000000 . . .
#> [4,] . 0.48770657 . . 0.05447533
#> [5,] . 0.05447533 . 0.05447533 .